Scalars
(ab)c = a(bc)
We learn the above in High School Algebra. To imagine why it is true, imagine a 3D array of dots with dimensions a,b and c. For (ab)c we can “slice it up” as having c “ab” rectangles and, assuming we have commutativity, a(bc) goes to (bc)a and now we have a “bc” rectangles.
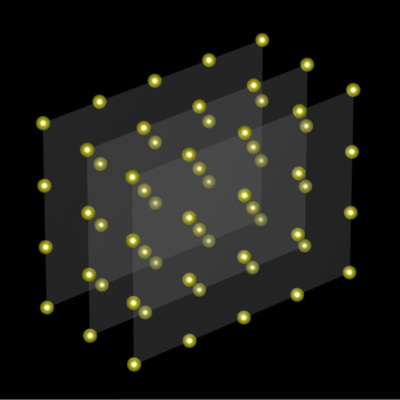
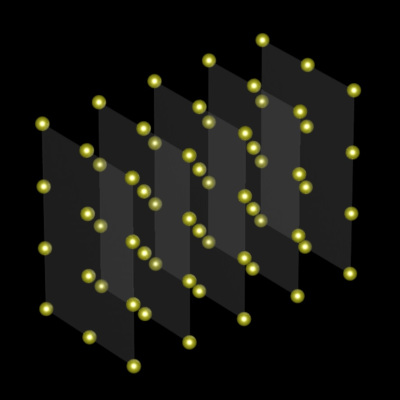
Matrix Multiplication
Matrix Multiplication is associative.
Summation
Summation is associative.
If we have three summations, we can view each term as being the piece in a cube and every piece is added together, and each of the three summations is responsible for one of the sides of the cube.