We are going to use the metric signature (-,+,+,+). The dot product of two four-vectors, and , can be expressed as: Here, represent the components of vector and represent the components of vector . Discussions on this topic will probably mention a Minkowski metric. We used… There is a matrix that corresponds to the MinkowskiContinue reading “Dot Product of Four Vectors”
Author Archives: Robert Sterling
Two Moments in Time
Our hypothesis here is that sometimes when you do a physics calculation and you get two answers and you recognize one as being sensible… …there might be something interesting about the “nonsense” answer. A student does a calculation and gets a positive answer and a negative answer and says “we can’t go back in time,Continue reading “Two Moments in Time”
Initial Conditions and Related Things
You are a secret agent. You have ten seconds to use your secret cell phone to tell everyone where you are located. Assume you know the vehicle has been traveling for two hours at 60 miles per hour eastward on a straight road that goes in the east direction. With what you know right nowContinue reading “Initial Conditions and Related Things”
The Road to Rindler
This story takes place in two dimensions, (t) and (x). We are choosing (-,+,+,+) for the signature of our metric. The color curves in the picture are hyperbolas. Our goal here is to show that we can start with several assumptions that we say are basic assumptions and get to two equations that contain hyperbolicContinue reading “The Road to Rindler”
Simultaneous Equations and Intersections
The more bizarre thing to say is “try to imagine that each simultaneous equation is a road of sorts in the space where the simultaneous equations exist, and the solution to the simultaneous equations is the intersection of the simultaneous equations.” Let’s hit it with a simpler example. Assume we have the “requirement” that x=4Continue reading “Simultaneous Equations and Intersections”
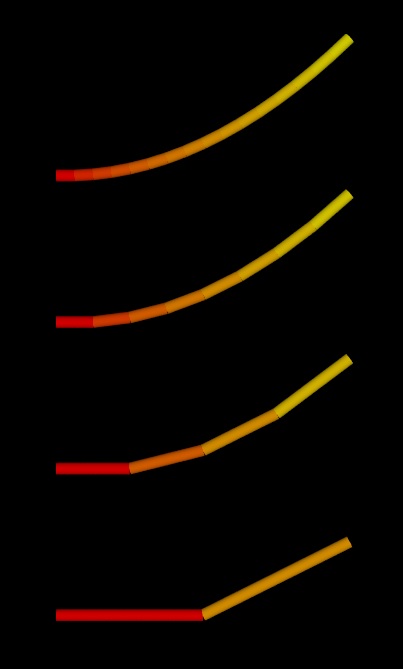
Seeing Curvature
Most of the time we will probably spot curvature by looking at a graph where both axes are linear and then noticing that what is plotted–linear it is not. But sometimes we could have a graph where one axis nonlinear and on the graph we see a straight line. This happens on the left inContinue reading “Seeing Curvature”
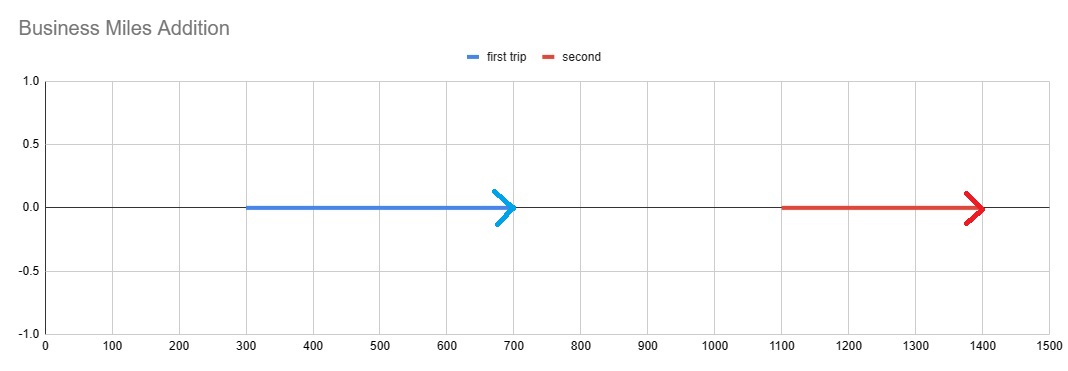
Business Miles Addition
The simple version of this story is that 400 + 300 = 700. We want you to walk away agreeing that there must be more to it than that. In vector everything, we say that we never just add numbers. Every term in a summation must be attached to something that is quantifiable (like quartersContinue reading “Business Miles Addition”
Components and Coordinates
The topic is muddled because if you read enough web pages you find people switching the words and this might make you think they are perfect synonyms. ChatGPT insists that they are not and it expounds on this to make the word component take you to one story and the word coordinate to take youContinue reading “Components and Coordinates”
Building a Function from Small Straight Line Segments
We want to tell the story of integration from a “start with a derivative” perspective. Let’s start by making you (the reader) the function y=x and we’ll give you the nickname “ex”. Yes, you are a function. Here’s the deal–you are somebody’s derivative. That’s right, some function somewhere says “yeah, ex is my derivative”. ThatContinue reading “Building a Function from Small Straight Line Segments”
Vectors
Vectors… Let’s talk about them. There will be almost no math here, we have that elsewhere. Our interest is almost entirely Physics. We argue that we chose the math we teach you because we discovered that it could explain our physical data. This is true at least for ‘displacement’, ‘viscosity’, ‘acceleration’, ‘force’, ‘momentum’, ‘energy’, ‘power’.Continue reading “Vectors”