There is no conflict between Math and Magic. In any event where it seems there is a conflict between Math and Magic, Magic is wrong. Throw it overboard. With that said, we find things in math which might seem to be a bit magical… We sometimes get the answers to our calculations for things withContinue reading “Magic in Math”
Author Archives: Robert Sterling
Newton’s Idea and Two Open Sets
Newton typed the following on his Apple IIe computer… Quantities, and the ratios of quantities, which in any finite time converge continually to equality, and before the end of that time approach nearer the one to the other than by any given difference, become ultimately equal. Any student of calculus should spend some time mullingContinue reading “Newton’s Idea and Two Open Sets”
Points in Different Coordinate Systems
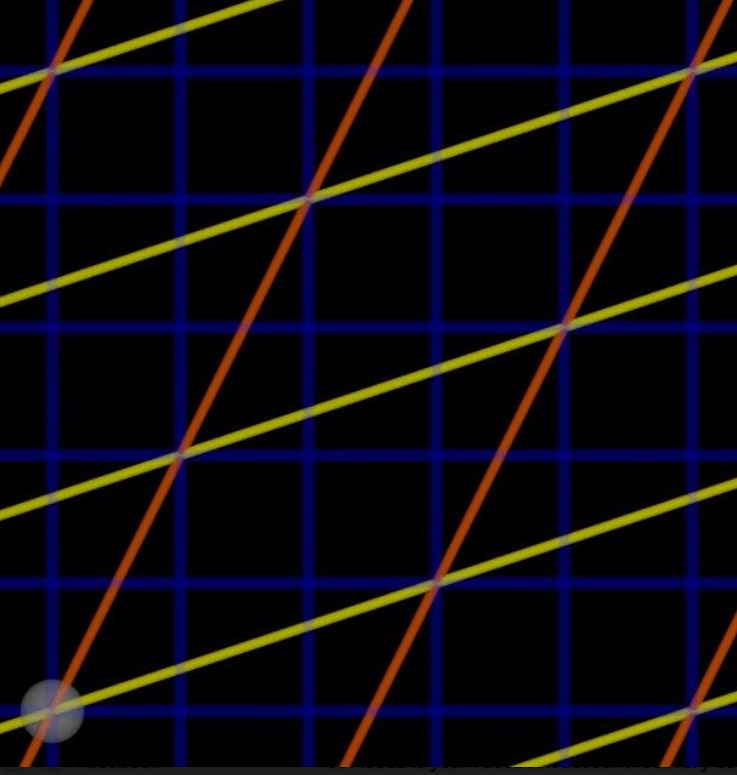
Find the point (3,1) using the (blue, blue) coordinate system. What is it in (yellow, orange)? answer below Find the point (1,2) using the (blue, blue) coordinate system. What is it in (yellow, orange)? answer below A larger picture is provided so you can find more points. You will soon be taking data and thenContinue reading “Points in Different Coordinate Systems”
Galilean Story
Galileo was familiar with several aspects of relativity. Galilean Relativity differs from Special Relativity in that Special Relativity is built around the idea that the speed of light is constant in all inertial frames of reference. In Galilean Relativity, if a flashlight on a train traveling 50 mph shoots a burst of light, the speedContinue reading “Galilean Story”
Galilean Transformations
We will be using the math developed in our blog post Galilean Story. Our goal will be to start with and finish with . The equations are shown below. We are going to take the equations above and start with… …and then make substitutions to slowly change the non-primed vectors and components to primed vectorsContinue reading “Galilean Transformations”
Fractions : Part Two
This is a longer post where we play with fractions and the intent is to take you to something you will see later when you learn about vectors, covectors and tensor calculus. Think about what you see on an inch ruler and then look at… …and with you imagination, tell yourself you are seeing… NowContinue reading “Fractions : Part Two”
Placeholders
We may have a story where we believe a 3×3 matrix is needed to convert a first thing to a second thing. We may choose a notation, a way of typing symbols, to build that 3×3 matrix even though we do not yet know what the numbers are. At this point we don’t know anyContinue reading “Placeholders”
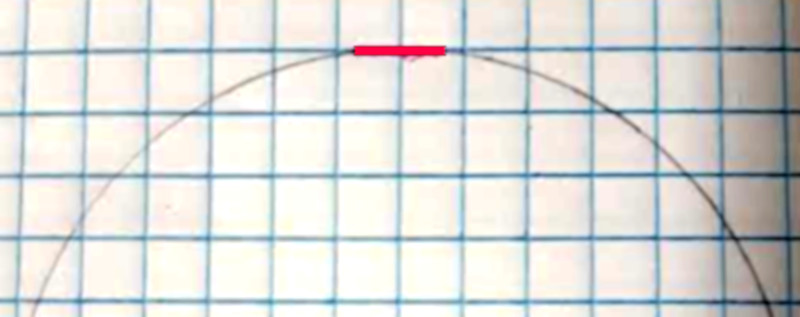
Flatness on a Curve
According to story, Newton encountered some ridicule when he broke the news on Calculus. If we can imagine him giving Power Point presentation to a conference, we might see him taking a hard question from the audience… “Isaac, is that dx zero or non-zero?” That dx is a butterfly we can’t catch. It is neverContinue reading “Flatness on a Curve”
Addition, Aggregation and Explosion
Aggregation is violent. If you have 2 Apples and you have 3 apples, and you light a cigarette lighter with a “+” on it between the two, there is a violent explosion and when the dust clears you have five apples. If we repeat this experiment with two apples and three oranges, nothing happens. OneContinue reading “Addition, Aggregation and Explosion”
Invariant Tensorship
OK, tensorship is not a word, but if you are an array that holds together a bunch of numbers, and you aspire be certified as a tensor, the will make you prove you are invariant to Your invariant character is why physicists will love you–after they stop hating you. Below is a small story thatContinue reading “Invariant Tensorship”