Mission Statement
Several ideas from Boolean Algebra will be briefly introduced. Our focus will be taking you to ideas in Boolean Algebra that will be helpful to you as you contemplate the basics we build on in our trek toward tensors. We are especially thinking of Distributivity. Finally, we hope you enjoy what you find here enough to pursue Boolean Algebra further on other web pages.
Values of True and False
Boolean Algebra concerns work with variables that can hold values of either true or false. No other values are possible, there is no neutral ground between the two.
Why would we do that? Computers and electronics love it!
Symbols for True and False
It is typical to use “1” as a shorthand for true and “0” as a shorthand for false. Please keep in mind that when this is done, we are using “1” as a symbol, a usage that is different from when we use it as an integer value greater than zero and less than two.
Operations
We can bring together variables in different ways, and we give the name “operations” to these ways. There are three operations in Boolean Algebra, “Conjunction”, “Disjunction” and “Negation”.
For Conjunction, the symbol is .
Let . We can read this in informal words as “C equals A and B”. In order for C to be true, A and B must both be true. If one or both is false, then C is false. We illustrate this in the table below:
For Disjunction, the symbol is .
Let . We can read this in informal words as “C equals A or B”. This time, C will be true in every case except for the one where both A is false and B is false. We illustrate this in the table below:
For Negation, the symol is .
Let . We can ready this in informal words as “C equals not A”. Because there are only two possible values (true or false) this guarantees that the value of C will be the opposite of the value of A. We illustrate this in the table below:
(there is content that belongs here, we’re skipping ahead to Appendix A, to show Distribution behaving differently than the way it behaves in Elementary Algebra (the Algebra that you learn in High School).
Appendix A
Skipping ahead… Two statements will be shown below without proof. We want one placed close to the other so you can easily compare them. After that, a Truth Table will be provided for each equation.
Conjunction Distributes over Disjunction
Disjunction Distributes over Conjunction
Equations and Truth Tables
Conjunction Distributes over Disjunction
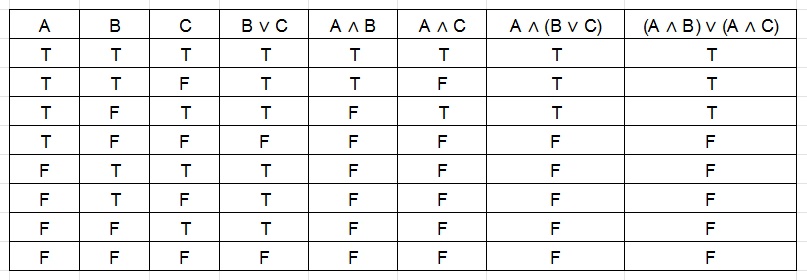
Disjunction Distributes over Conjunction
