Future Content

We hope in a few weeks to have a path cleared from Vectors to Tensors.

A more fun approach is available at Chasing Rabbits. This borrows some of the fun from the story of Alice in Wonderland and also makes use of the song “White Rabbit” by Jefferson Airplane. We’ve decided to maintain a page with links to several references that have proven helpful time and again.

Some artwork has been prepared to go with the ideas;

Assume that the cubes are components that contain values.

In the above illustration, two mathematical objects are brought together for a multiplication.

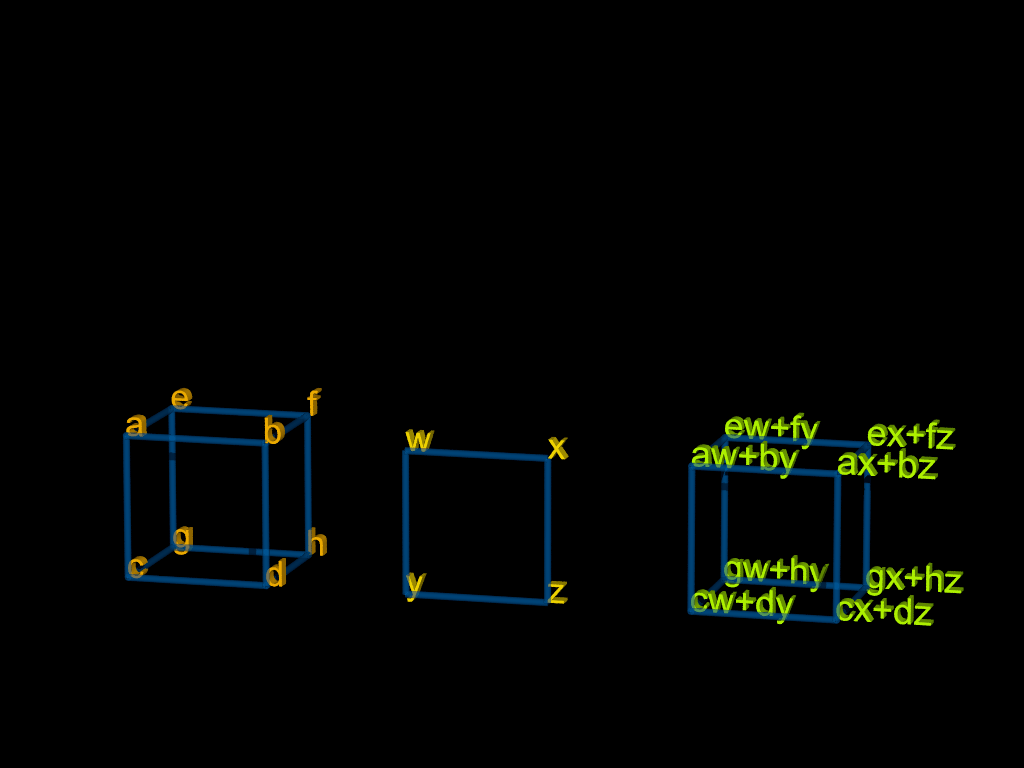
A tensor and a matrix are multiplied together.

For the above example showing a tensor being multiplied by a matrix, notice that we can think of the tensor as containing two matrices and the result is a tensor built from two matrices.

The above is under investigation — the idea is a concept and we are looking to confirm that it matches the standard convention. Alternately, if it is one of several accepted conventions, we will try to give it appropriate labeling to reflect which choice was used.

f(x,y)=xy

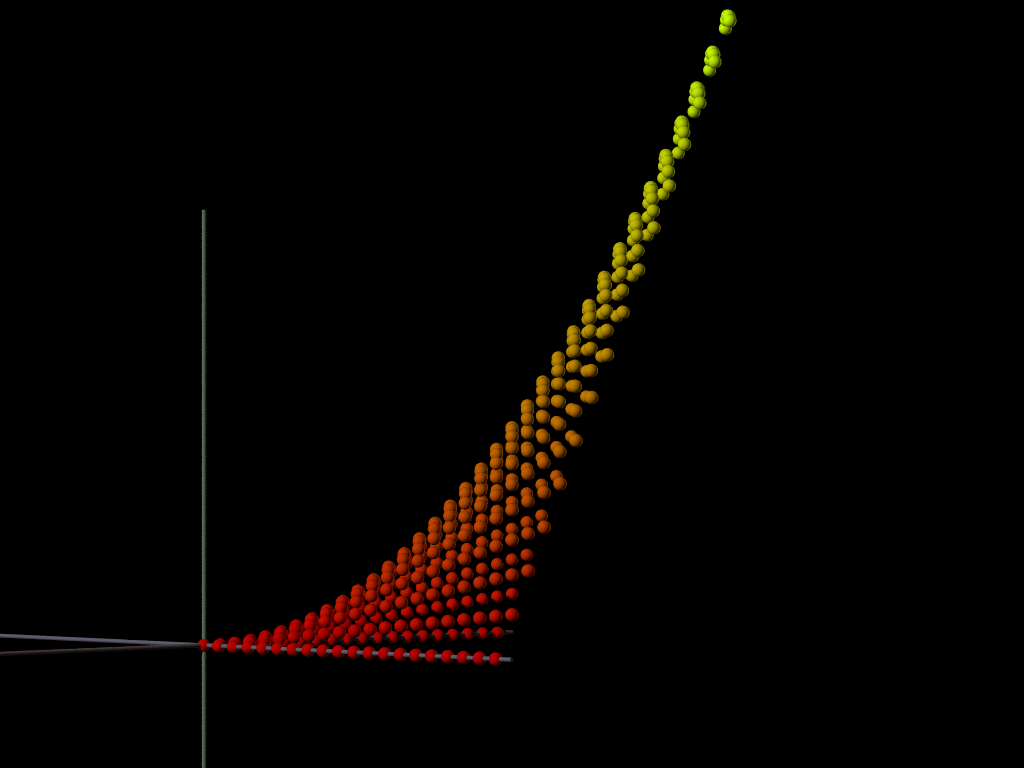
The above illustration graphs the points of f(x,y) = xy. The equation is Bilinear. Slices over lines parallel to an axis are straight lines, but we can see that other slices, such as a slice over the line y=x, have curvature.

We will be discussing Covariant and Contravariant when we start delving further into Tensors.

A comment was found suggesting that we can create tensors from vectors and covectors. We will see if we can follow further on this.

Basis and cobasis coincide only when the basis is orthogonal.

We found that for contravariant vectors:

v'^{\mu} = av^\mu

v'_\mu = \dfrac {1}{a} v_\mu

Notation

If we multiply matrix ij against vector j we end up with vector i.

If we multiply ijkl against jl will we end up with ik?

Is there a rule that we only take out one letter at a time?

Is there also a rule that it doesn’t matter which letters we do first, the results will come out the same?

Matrix of Partials

I found it before, I can’t find it now. I will list the references that I have checked:

Porat wrote the following:

S^i_j = \dfrac {\partial x^j}{\partial y^i}

T^m_k = \dfrac {\partial y^m}{\partial x^k}

T^m_j S^j_i = \delta^m_i

Later he wrote

v^i = \dfrac {\partial x^i} {\partial \tilde x^j} \tilde v^j

\tilde v^i = \dfrac {\partial \tilde x^i} {\partial x^j} v^j

From what we know about matrix multiplication and the fact that each new vector component is a linear combination of all the old Vector components we can build the matrix shown below:

\begin{bmatrix} \dfrac {\partial \tilde x^1} {\partial x^1} & \dfrac {\partial \tilde x^1} {\partial x^2} & \dfrac {\partial \tilde x^1} {\partial x^3} \\ \\ \dfrac {\partial \tilde x^2} {\partial x^1} & \dfrac {\partial \tilde x^2} {\partial x^2} & \dfrac {\partial \tilde x^2} {\partial x^3} \\ \\ \dfrac {\partial \tilde x^3} {\partial x^1} & \dfrac {\partial \tilde x^3} {\partial x^2} & \dfrac {\partial \tilde x^3} {\partial x^3} \end{bmatrix}

What are our Top Five Features?

  1. Using a computer program to explain tensor multiplication.
  2. Our willingness to show representations for tensors of rank 3 or higher and our explanation of why these are not needed.
  3. Our mention t
  4. w