Pythagorean Theorem

Assume a right triangle where the hypotenuse is labeled ‘c’ and the other two sides are labeled ‘a’ and ‘b’.

You can test this by drawing lengths four and three perpendicular to each other (the perpendicularity is required to make what you are drawing a right triangle) and then drawing the length between their ends, measuring it, and finding that it has a length of 5.

25 = 16 + 9

The above is just a test, it isn’t a proof, but if you want a proof, consider what we have below:

For any right triangle with sides a,b and hypotenuse c (see below on the left), if we put two copies of the triangle together, we have a rectangle with sides a and b, and thus it has area ab. Considering this, if we have four of these triangles, the total area is 2ab.

Now, put these four triangles (which have area 2ab) together in the way that is shown below on the right.

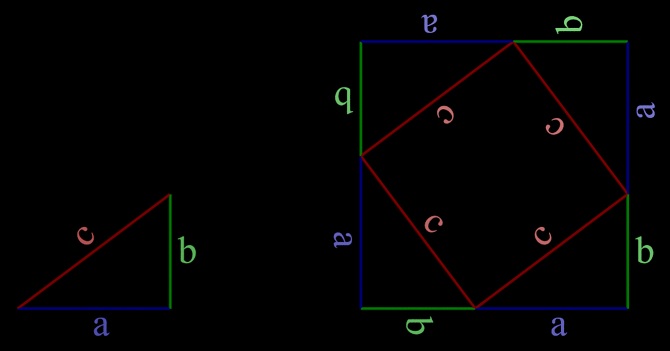
Now, put these four triangles (which have area 2ab) together in the way that is shown below on the right. Look in the empty area enclosed by the four triangles–can you see that it is a square with area ? If yes, then we can say that we’ve created a large square with area (2ab + .

But wait, we know even more… Each side of this new large square has a length of a+b. We can calculate the area of this large square as . We can solve for this using the binomial multiplication that we learned in Algebra.

So at this point we have two different calculations that give the area of the large square. Since these two calculations are equal, we can use them to build an equality.

The above equality is correct, but we notice we can simplify it by removing a term present on both sides (the 2ab). We do this and get the followig:

We have just proven the Pythagorean Theorem!