Pythagorean Theorem

Assume that we have a Right Triangle and we label the side that is the hypotenuse with c and we label the other sides with a and b.

$c^2 = a^2 + b^2$

This equation can be proven by constructing four right triangles that are equal and placing them together in a way that creates a square with sides of length c inside another square. This is shown below:

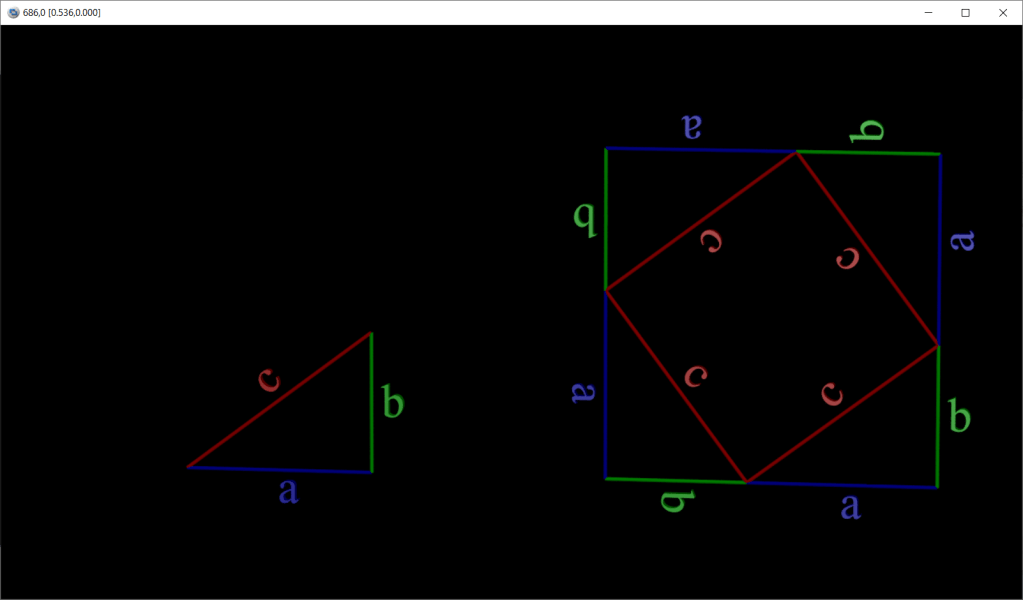
The bigger square has an area of $(ab)^2$ . The smaller square has an area of $c^2$ .

Each right triangle has an area of $\dfrac {1}{2}ab$ .

We get the bigger square when we add together the smaller square and 4 of the right triangles.

$(ab)^2 = c^2 + 4\\dfrac{1}{2}ab$

We can expand the left side and combine scalars on the right side:

$a^2 + 2ab + b^2 = c^2 + 2ab$

We can cancel the term that appears on both sides:

$a^2 + b^2 = c^2$

Share this: