Robert and Sines

For an extreme right triangle that has the angle approaching 90 degrees, the length of the adjacent side is approaching 0 and the length of the opposite side is approaching the length of the hypotenuse.

From these observations we can discover that as we approach 90°, sine is approaching one and cosine is approaching zero.

For an extreme right triangle that has the angle approaching 0 degrees, the length of the adjacent side is approaching the length of the hypotenuse and the length of the opposite side is approaching zero.

From these observations we can discover that as we approach 0°, sine is approaching zero and cosine is approaching one.

Appendix T – what to buy from the Trigonometry Store

We start by buying the formulas that give us cosine from sine and tangent from sine and cosine.

Sine-based Definitions

In degrees:

Cos(x) = Sin(90+x)

tan(x) = \dfrac {Sin(x)} {Cos(x)}

If we have both sine and cosine, we can calculate tangent:

  • Sine = \dfrac {opposite}{hypotenuse}
  • Cosine = \dfrac {adjacent}{hypotenuse}

The above ratios can be put together:

  • \dfrac {opposite}{hypotenuse} * \dfrac{hypotenuse}{adjacent} = \dfrac{opposite}{adjacent}

Alternate Interior Angle Equality

If a transversal line intersects two parallel lines we get two sets of alternate interior angles.

Alternate interior angles are equal.

To prove this we need “Corresponding Angles Equal” and “Complements of Equal Angles are Equal.

Triangle Sum of Angles

The three angles of a triangle always add up to 180 degrees.

This can be shown by cutting parallel lines with two transversals in a way that builds a triangle and then using corresponding angle equality to show that we get 180 degrees.

We get a corollary from this– if the triangle is a right triangle then the two remaining angles add up to 90 degrees. Those two angles are Complementary Angles.

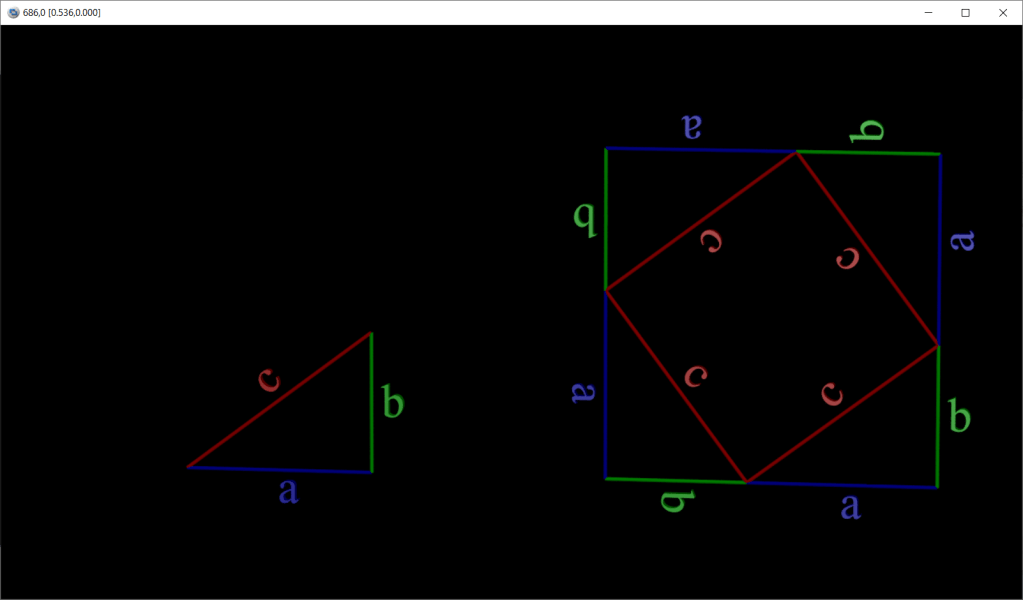
For a Right Triangle, if we give the hypotenuse the letter ‘c’, and we give the letters ‘a’ and ‘b’ to the other two sides then:

a^2 + b^2 = c^2

The above can be seen in the a drawing that uses four right triangles to build to squares.

(a+b)^2 = 2ab + c^2

Proving the 30 60 90 Triangle

Start with an Equilateral Triangle and bissect it. Every angle of the triangle has an angle of 60°. Device section Cuts this feature to 30° angles. If every side of equilateral triangle has a length of 2 in the bisection cuts one besides into two pieces with lengths of 1 each.

Cosine – Getting a Half Angle

cos (2 \theta) = 2 cos^2 (\theta) - 1

\dfrac { cos (2 \theta) + 1}{2} = cos^2 (\theta)

cos (\theta) =\sqrt {\dfrac { cos (2 \theta) + 1}{2} }

The first equation lets us calculate cos 20 if we know cos 10 and the last equation lets us calculate cos 10 if we know cosine 20.

Our goal is sines, so we need to do tricks like finding cos(80) when we want sin(10).